Посвящается Nastenke – истинному украшению forum.sources.ru
Автор: Math
|
«Тензорное
исчисление является истинным языком, в основе которого лежат интуитивные
(визуальные) образы, хорошо знакомые даже тем, кто никогда не слышал слов
вектор или тензор.»
П.А. Жилин |
Эта статья открывает серию статей посвященных способам описания вращательного движения в трехмерном эвклидовом пространстве. Статья ориентирована на широкий круг читателей, желающих узнать простые, интуитивно понятные и в то же время одни из самых мощных математических средств задания пространственной ориентации абсолютно твердого тела. Для чтения статьи достаточно знаний по математике в объеме школьной программы (хотя в некоторых случаях понадобятся минимальные знания из линейной алгебры). Желательно, чтобы читатель имел устойчивое представление о том, что такое векторы и какие операции с ними можно производить. В статье не приводятся полные доказательства теорем, т.к. они достаточно громоздки, хотя и не трудны. Даются лишь необходимые для понимания пояснения. Также приводятся без доказательства ряд важных тождеств, доказательство которых вполне посильно проницательному читателю, что мы и рекомендуем проделать. Статья будет полезна в первую очередь людям, занимающимся программированием 3D графики.
В статье рассказывается о таких средствах как тензор поворота, вектор конечного поворота, кватернионы, а также показывается неразрывная связь между этими тремя объектами. В различных ситуациях удобнее пользоваться либо тем, либо другим средством. Но ни в коем случае нельзя впадать в крайность, предпочтя одно средство всем остальным. Мы в данной статье намеренно уклонились от описания координатного представления векторов и тензоров, дабы стимулировать читателя к чисто интуитивному восприятию данных объектов. Координатная форма будет дана в следующей статье, посвященной многим знакомым матрицам поворота. Причина этому следующая. Матрицы поворота являются лишь маскировкой, которая ничего, кроме неясности в трактовки не вносит. Попробуйте, например, попросить человека написать без шпаргалки матрицу поворота вокруг произвольной оси на произвольный угол. Тем, кому это под силу, нет нужды читать эту статью. Те же, кто прочитает эту и следующую нашу статью, научатся это делать в течение нескольких минут.
Пусть читатель не удивляется и простит автора за то, что статья написана от третьего лица, так как будто бы автор весь излагаемый материал сам придумал. Отнюдь нет. В хороших книгах, правда их немного, можно найти гораздо более качественное изложение. Просто автор считает, что статья, написанная в безличной форме, может отпугнуть впервые изучающего данный предмет, т.к. бесконечные фразы типа «в математике рассматривается…» и т.п. оставляют у читателя чувство неуверенности в полученных знаниях и необходимости обращения к дополнительной литературе, в которой подчас нет никакой надобности.
Развитие всей рациональной науки на протяжении столетий необходимо сопровождалось развитием, не всегда осознанным, тензорного языка, процесс становления которого был очень длительным и трудным. Например, понятие вектора было введено Саймоном Стевином (S. Stevin) в 1580 году, но первые учебники по механике, использующие векторный язык, появились только в начале XX века.
Тензоры второго ранга (тензор поворота, тензор инерции твердого тела) впервые были введены Леонардом Эйлером (Leonhard Euler) в 1758 году. Термин «тензор», однако, был введен лишь в 1900 году по предложению В. Фойгта (W. Voigt). Тем не менее, Л. Эйлер работал с этими объектами как с тензорами. Важно подчеркнуть, что Л. Эйлер на формальном уровне не владел многими стандартными ныне методами. Однако, по числу новых фундаментальных результатов ему нет равных в истории человечества, за исключением разве что Архимеда. В огромной степени это объясняется тем, что Л. Эйлер обладал совершенно феноменальной интуицией, т.е. способностью непосредственного визуального восприятия образов вводимых им объектов.
В физике используется огромное множество различных понятий. Это неизбежно приводит к необходимости их классификации. Наиболее общей является классификация по так называемому тензорному признаку, так как все понятия, описывающие количественные характеристики физических объектов, являются тензорами, но тензорами различных рангов. Тензоры нулевого ранга называются скалярами. Тензоры первого ранга называются векторами. Эти два типа тензоров хорошо известны из школьных курсов математики и физики. Тем не менее, кратко напомним их определения и основные операции над ними.
Определение: физические величины, которые полностью характеризуются заданием одного вещественного числа, не зависящего от выбора системы координат, называются скалярами.
Примерами скаляров являются масса, объем, температура. Координаты вектора, однако, нельзя назвать скалярами, т.к. координаты вектора меняются при замене системы координат (смене базиса).
Следующей после скаляров ступенькой в классификации физических величин являются векторы или тензоры первого ранга. Векторы являются не столько математическими изобретениями, сколько элементами нашего интуитивного мышления.
В Природе существуют, по крайней мере, два принципиально несводимых друг к другу вида движения тел. Первый тип движения характеризует перенос (трансляцию) тела в пространстве. Второй тип характеризует изменение ориентации тела в пространстве. Оба типа движения интуитивно понятны человеку с рождения. Одной из причин такой понятности, возможно, является то, что человек начиная с эмбрионального состояния, вынужден совершать оба типа движений.
Соответственно двум типам движения существуют две формальные логические конструкции отображения объективной реальности. Это направленный отрезок (прямой вектор) и спин-вектор.
Два примера. Первый. Любой нормальный человек, например, гуляя по парку и увидев стрелку-указатель с надписью «Кафе 100 м» поймет, что нужно делать. Второй. Предложите группе людей, не математиков и не физиков, например, филологов, схематически изобразить на листке бумаги движение обычного вращающегося волчка. В «сухом остатке» у большинства картина будет примерно такой, как на рис. 1.

Рис. 1. Спин-вектор
Подведем итог. Чтобы задать направленный отрезок (прямой вектор), необходимо указать в физическом трехмерном пространстве (системе отсчета) направление и вещественное число (скаляр), называемое длиной (модулем) вектора. Чтобы задать спин-вектор, необходимо в физическом трехмерном пространстве задать прямую, называемую осью спин-вектора, затем указать направление вращения и поставить в соответствие данной конструкции вещественное число, называемое длиной (модулем) спин вектора. Данное число может характеризовать не только угол поворота, но и скорость поворота, и т.д.
Однако работать с двумя объектами различной природы неудобно. Тем более, что спин-векторам можно взаимно однозначно сопоставить прямые векторы, введя дополнительное соглашение, называемое ориентацией системы отсчета.
Пусть дан спин-вектор a*. Сопоставим ему прямой вектор a по следующим правилам:
а) вектор a расположен на оси спин-вектора a*;
б) модуль a равен модулю a*;
в) вектор a направлен так, чтобы при взгляде с его конца круговая стрелка показывала вращение против хода часовой стрелки;
либо
г) вектор a направлен так, чтобы при взгляде с его конца круговая стрелка показывала вращение по ходу часовой стрелки.
Выбор одной из двух возможностей называется ориентацией системы отсчета. Важно осознать, что Природа ничего не знает о нашем произволе. Поэтому в используемых нами математических конструкциях для описания объективной реальности должны существовать средства компенсации данного произвола. Как мы увидим, основной объект обсуждения данной статьи – тензор поворота – не зависит от ориентации системы отсчета.
Определение: система отсчета называется называется правоориентированной, если трансляции и вращения в ней согласованы в соответствии с правилами а), б) и в). Система отсчета называется левоориентированной, если трансляции и вращения в ней согласованы в соответствии с правилами а), б) и г).
Таким образом, в ориентированной системе отсчета мы можем работать только с одним множеством объектов: множеством направленных отрезков. Однако в этом множестве все равно сохраняется различие между истинно прямыми и псевдопрямыми векторами, прообразами которых служат спин-векторы.
Для первого знакомства достаточно сказанных весьма общих слов про прямые и псевдопрямые векторы. Чтобы не уходить в сторону от главной задачи, оставим пока эту тему. Глубинное понимание различия понадобится лишь при введении понятия угловой скорости, что, возможно, будет сделано в одной из наших следующих статей.
Выше было введено в рассмотрение множество направленных отрезков. Для математики и физики интерес представляют только такие множества, на которых удается ввести дополнительные структуры, а именно, законы композиции элементов множества, или по-другому операции над элементами множества. Для векторов вводятся четыре основных операции. Мы надеемся, что читатель имеет твердое представление об этих операциях. При этом для целей нашей статьи важна именно геометрическая трактовка оных. Напомним лишь кратко основные операции над векторами
Примем, что вектору c можно однозначно сопоставить пару векторов a и b по правилам параллелограмма или треугольника. Вектор c называется суммой векторов a и b
| c = a + b | (1) |
Можно доказать, что операция сложения векторов коммутативна
| a + b = b + a, |
и ассоциативна
| (a + b) + c = a + (b + c). |
Примем, что любому скаляру α и любому вектору b можно однозначно сопоставить вектор a, который обозначается a = αb, такой, что справедливы утверждения
а) a = α b;
б) если α > 0, то направление a совпадает направлением b, если α < 0, то направление a противоположно направлению b.
Можно доказать справедливость соотношений
α(a + b) = αa + αb,
(α + β)a = αa + βa.
Примем, что каждой паре векторов a и b можно однозначно сопоставить скаляр α, который обозначается a · b и вычисляется по правилу
| α ≡ a · b = a b cos θ, | (2) |
где θ – угол между векторами a и b. Можно доказать, что скалярное произведение коммутативно
| a · b = b · a. |
и дистрибутивно
| a · (b + c) = a · b + a · c. |
Определение: два вектора a и b называются ортогональными, если их скалярное a · b произведение равно нулю.
Первые три закона композиции имеют место как в ориентированной, так и не в ориентированной системе отсчета. Четвертый закон композиции имеет место только в ориентированной системе отсчета.
Векторное произведение введем в два этапа. Пусть дана упорядоченная пара векторов a и b, где a считается первым (левым) сомножителем, а вектор b – вторым (правым). Сопоставим векторам a и b спин-вектор c* такой, что
а) ось вектора c* ортогональна плоскости, натянутой на векторы a и b;
б) круговая стрелка показывает направление кратчайшего поворота от вектора a к вектору b;
в) модуль спин-вектора c* равен
| c* = a b sin θ, | (3) |
где θ – угол кратчайшего поворота от a к b.
Для спин-вектора c* введем обозначение c* = [a, b]. Сразу можно отметить, что c* = [a, b] = –[a, b]. Теперь осталось спин-вектору c* поставить в соответствие прямой вектор c. Это можно сделать двумя способами в зависимости от выбранной нами ориентации в системе отсчета. Если мы работаем в правоориентированной системе отсчета, то при взляде с конца вектора c поворот от a к b будет осуществляться против часовой стрелки. Если же мы работаем в левоориентированной системе отсчета, то при взляде с конца вектора c поворот от a к b будет осуществляться по часовой стрелке. Чтобы не вносить путаницу, условимся всегда работать в правоориентированной системе отсчета.
Свойства векторного произведения:
а) a × b = – b × a;
б) a × (b + c) = a × b + a × c – дистрибутивность;
в) (a × b) × c ≠ a × (b × c) – ассоциативности нет!
Полезные тождества:
а) (a × b) · c = (b × c) · a = (c × a) · b – циклическая перестановка векторов в смешанном произведении не меняет результат произведения;
б) a × (b × c) = b(a · c) – c(a · b) – правило «бац минус цаб».
Тензоры нулевого ранга (скаляры) и тензоры первого ранга (векторы) не исчерпывают списка необходимых для физики и, в частности, механики понятий. Необходимы и более сложные конструкции – тензоры высших рангов. На интуитивном уровне тензоры ощущаются уже не столь отчетливо, как скаляры и векторы. Поэтому требуется определенная тренировка на уровне логического мышления, прежде чем исчезнет неудобство, связанное с восприятием тензора второго ранга, как чисто формального объекта.
Для целей данной статьи нам необходимо научиться работать с парами векторов, рассматриваемых как единое целое и называемых диадами. Упорядоченную пару векторов ab будем называть диадой. Термин «упорядоченность» означает, что порядок следования векторов в диаде важен
| ab ≠ ba. |
Точно также как и для векторов, для того, чтобы множество диад представляло реальный интерес нужно ввести на этом множестве законы композиции элементов (операции над элементами). Прежде всего, введем операции произведения диады на вещественное число и операцию суммы диад.
Произведением диады ab на вещественное число α называется диада, вычисляемая по правилу
| α(ab) = (α a)b = a(αb) = αab . | (4) |
Аксиома:
| (α + β)ab = αab + βab. | (5) |
Из (4) при α = 0 имеем
| 0ab = 0b = a0. |
Из (5) при α = 1 и β = 0 имеем
| ab = (1+0)ab = 1ab + 0ab = ab. |
Поэтому диаду 0ab = 0b = a0 называют нулевой диадой: ее добавление к произвольной диаде ab не меняет диады ab.
Далее примем правила сложения диад с одинаковыми правыми (левыми) сомножителями
|
a (b + c) = ab + ac
,
(a + b)c = ac + bc. |
(6) |
Но что, к примеру, означает «сумма»
| ab + cd ? |
Оказывается в множестве диад данную операцию не определить. Необходимо расширить множество. Будем рассматривать множество неупорядоченных совокупностей трех упорядоченных пар векторов. Во сказанул!!! Не имея возможности объяснить более подробно, скажем, что именно на множестве таких элементов можно определить операцию суммы, не выводящую за пределы множества. Также можно показать, что сумма (неупорядоченная совокупность) конечного числа упорядоченных пар векторов (диад) сводится к совокупности не более чем трех диад.
Определение: Тензором второго ранга в трехмерном пространстве называется неупорядоченная совокупность конечного числа упорядоченных пар векторов (диад)
| A = ab + cd + ... + mn. | (7) |
«Неупорядоченная совокупность» означает, что порядок слагаемых может быть произвольным. Заметим, что стремиться свести (7) к совокупности трех диад не только не нужно, но и, как правило, это нецелесообразно.
Выше уже были введены операции сложения тензоров и умножения тензора второго ранга на число. Введем еще ряд операций. Мы дадим не совсем строгие определения, а только необходимый минимум для понимания происходящего на примере диад.
Двум тензорам второго ранга A = ab и B = cd поставим в соответствие тензор C по правилу
| C = A·B = (ab)·(cd) = (b · c)ad. | (8) |
Внутреннее умножение не коммутативно A·B ≠ B·A, т.к.
| B·A = (cd)·(ab) = (d·a)cb. | (9) |
Внутреннее умножение ассоциативно
| (A·B)·C = A·(B·C) = A·B·C |
и дистрибутивно
| (A + B)·(C + D) = A·C + A·D + B·C + B·D. |
Двум тензорам второго ранга A = ab и B = cd поставим в соответствие число α по правилу
| α = A··B = (ab)··(cd) = (b · c)(a · d). | (10) |
Двойное внутреннее умножение коммутативно
| A··B = B··A |
и дистрибутивно
| (A + B)··(C + D) = A··C + A··D + B··C + B··D. |
Тензору A = ab поставим в соответствие тензор, построенный по правилу
| AT = (ab)T = ba. | (11) |
Двум тензорам второго ранга A = ab и B = cd поставим в соответствие число α по правилу
| α(A, B) = A··BT = (ab)··(cd)T = (b · d)(a · c). | (12) |
Важное свойство скалярного произведения, отличающее его от двойного внутреннего
| A··AT = 0 => A = 0. | (13) |
Скалярное произведение коммутативно α(A, B) = α(B, A) = B··AT.
Поставив тензору A = ab и вектору c вектор по правилу
| A · c = a(b · c) = ab · c, | (14) |
мы получим произведение тензора на вектор справа. Если же используется правило
| c · A = (c · a)b = c · ab, | (15) |
то говорят, что задано произведение на вектор слева.
Важно:
| A · c ≠ c · A, | |
| A · c = c · AT. |
Определение: тензор второго ранга 1 называется единичным, если для любого вектора x справедливо равенство
| x · 1 = 1 · x = x, | (16) |
Для любого тензора A справедливо тождество
| A · 1 = 1 · A = A. |
Аналогично скалярному вводятся векторные произведения справа и слева
| A × c = a(b × c) = ab × c, | (17) |
| c × A = (c × a)b = c × ab, | (18) |
результатом является тензор второго ранга.
Полезные тождества
| A × c = – [c × AT] T, | |
| a × 1 × b = ba – (b · a)1. |
Пусть тензор A есть совокупность диад
| A = ab + … + cd | (19) |
Следом тензора («tr» от trace, «Sp» от Spur – иногда можно встретить в немецкоязычной литературе) называется число, вычисляемое по правилу
| tr A = Sp A = a · b + … + c · d. | (20) |
Справедливы тождества trA = trAT, tr(A·B) = tr(B·A) = A··B, tr(A·B) = tr(AT·BT).
Пусть тензор A есть совокупность диад
| A = ab + … + cd. | (21) |
Векторным инвариантом тензора называется вектор, вычисляемый по правилу
| A × = a × b + … + c × d. | (22) |
Полезное тождество (a × 1)× = –2a.
Определение: тензор второго ранга называется симметричным, если он удовлетворяет равенству
| A = AT. | (23) |
Примеры симметричных тензоров второго ранга:
| aa , ab + ba, 1. |
Определение: тензор второго ранга называется антисимметричным, если он удовлетворяет равенству
| A = – AT. | (24) |
Примером антисимметричного тензора является тензор ab – ba.
Теорема. Любой антисимметричный тензор представим в виде
| A = a × 1 = 1 × a, A = – AT, | (25) |
где вектор a называется сопутствующим вектором тензора A.
Полезное и важное тождество
| a = – (1/2) A×. |
Важным классом тензоров второго ранга являются так называемые ортогональные тензоры.
Определение: тензор второго ранга Q называется ортогональным, если выполняется равенство
| Q·QT = 1. | (26) |
Легко показать, что линейное преобразование y = Q · x не меняет длин векторов, то есть | y | = | x |. Этот факт также может быть положен в основу определения ортогонального тензора. Из (26) следует, что тензор Q невырожден, т.к.
| Q–1 = QT, | (27) |
а транспонированный тензор существует всегда. Вычислим определитель Q
| det 1 = det(Q·QT) = (det(Q))2 = 1 => detQ = ±1. | (28) |
Таким образом, все множество ортогональных тензоров разбивается на два подмножества. Элементы множества тензоров, у которых detQ = +1, называются собственно ортогональными тензорами или тензорами поворота. Произвольный ортогональный тензор либо является тензором поворота, либо произведением тензора поворота на тензор инверсии (–1).
Как уже было сказано, тензор поворота не меняет длин векторов. А что происходит с углами? Пусть
| a ′ = Q · a, b ′ = Q · b. | (29) |
Тогда
| a ′ · b′ = a · QT·Q · b = a · b. | (30) |
Т.е. при действии тензора поворота на два вектора углы между ними сохраняются. Почему же у истинного тензора поворота detQ = +1? Ответ таков, в этом случае происходит только поворот, в случае же detQ = –1 происходит поворот с отражением.
Одним из наиболее простых общих представлений тензора поворота является следующее. Возьмем произвольную ортонормированную тройку векторов d1, d2, d3. При действии тензора Q они переходят также в ортонормированную тройку D1, D2, D3:
| Di = Q · di => Didi = (Q · di)di = Q·(didi) = Q·1 = Q. | (31) |
В формуле (31) использовано так называемое правило суммирования по Эйнштейну. Подразумевается суммирование от 1 до 3 по повторяющемуся индексу. Например,
| didi = d1d1 + d2d2 + d3d3. |
В (31) использовано общее представление единичного тензора didi = 1. Чтобы объяснить, почему этот так нужно перейти от прямого тензорного представления к координатному. В этой статье мы этого не делаем, и надеемся, что читатель поверит нам на слово. Таким образом, достаточно общим представлением тензора поворота является
| Q = Didi = D1d1 + D2d2 + D3d3. | (32) |
Это представление понадобится нам при доказательстве теоремы Эйлера. А сейчас мы хотим обратить внимание на одно полезное тождество, справедливое для любого вектора a и тензора поворота Q
| Q · (a × 1) · QT = (Q · a) × 1. | (33) |
Приведем пояснения к доказательству базовой теоремы в теории поворотов. Все остальные результаты теории получаются как следствия данной теоремы и при желании могут быть доказаны проницательным читателем самостоятельно.
Теорема Эйлера: произвольный тензор поворота P, отличный от 1, допускает единственное представление
| P = mm + cosθ(1 – mm) + sinθm × 1, | (34) |
где единичный вектор m определяет прямую в пространстве, называемую осью поворота; θ называется углом поворота и считается положительным, если поворот при взгляде с конца вектора m происходит против хода часовой стрелки.
Пояснения к доказательству: Покажем, что для тензора поворота P, существует единственный с точностью до множителя (±1) единичный вектор m (он называется неподвижным вектором тензора P), удовлетворяющий уравнению
| P · m = m, | m | = 1. | (35) |
Данное уравнение можно переписать в эквивалентной форме
| (P – 1) · m = 0, | m | = 1, | (36) |
т.е. вектор m является решением однородного линейного уравнения. Из курса линейной алгебры известно, что однородная система линейных алгебраических уравнений имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю
| det(P – 1) = 0. | (37) |
Покажем, что это так. Для этого выпишем цепочку тождественных преобразований (использовано det(P) = 1)
|
det(P – 1)
= det[P·(1 – PT)]
=
= det(P)det(1 – PT) = det(1 – PT) = = det(1 – P) = – det(P – 1). |
(38) |
Получили, что det(P – 1) = –det(P – 1), а это возможно, если верно равенство (37). Итак, ненулевое решение уравнения (36) существует. Понятно, что если m есть решение (36), то и (–m) есть решение этого уравнения. Однако оба эти вектора определяют одну и ту же прямую, натянутую на вектор m.
Далее методом «от противного» можно показать, что для тензора поворота P, отличного от 1, существует только один неподвижный вектор ± m.
Выберем теперь правую ортонормированную тройку векторов d1 = m, d2, d3. Согласно (32) мы можем записать
| P = D1d1 + D2d2 + D3d3 = D1m + D2d2 + D3d3, | (39) |
где тройка D1, D2, D3 также является правой ортонормированной. Умножив равенство (39) скалярно на m справа и учтя (35), получим
| P · m = D1 = m. | (40) |
Таким образом, равенство (39) принимает вид
| P = mm + D2d2 + D3d3. | (41) |
Здесь все четыре вектора d2, d3, D2, D3 лежат в одной плоскости, т.к. все они ортогональны одному и тому же вектору m. Поэтому D2, D3 можно разложить по векторам d2, d3 (см. рис. 2)
| D2 = cosθd2 + sinθd3, D3 = – sinθd2 + cosθd3. | (42) |
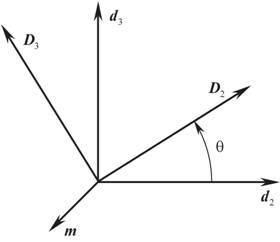
Рис. 2
Подставляя эти разложения в (41) и проводя элементарные преобразования, получаем
|
P = mm + (cosθd2 +
sinθd3)d2 +
(–sinθd2 + cosθd3)d3
=
= mm + cosθ(d2d2 + d3d3) + sinθ(d3d2 – d2d3) = = mm + cosθ(d1d1 + d2d2 + d3d3 – mm) + sinθm × (d1d1 + d2d2 + d3d3) = = mm + cosθ(1 – mm) + sinθm × 1 |
(43) |
Последним равенством и заканчивается доказательство теоремы Эйлера. Обратим внимание, что замена m на – m влечет за собой замену θ на – θ. При этом сам тензор P не меняется.
Пример.
Пусть вектор a параллелен оси поворота (лежит на оси поворота), т.е. a = αm, то P · a = a и вектор a не меняется при действии на него тензора P. Пусть a ортогонален оси поворота: a · m = 0. Тогда
| a′ = P · a = cosθa + sinθm × a. | (44) |
Этот результат изображен на рис. 3а.
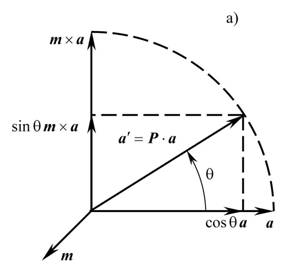
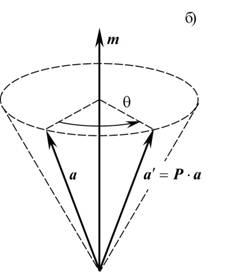
Рис. 3
Видно, что действие тензора поворота на вектор a, ортогональный оси поворота, сводится к повороту на угол θ вокруг m. Если θ > 0, то поворот производится против часовой стрелки при взгляде с конца m. Поворот произвольного вектора a показан на рис. 3б, при этом проекция вектора a на m сохраняется, а часть вектора a, ортогональная a, поворачивается на угол θ вокруг m.
Введем в рассмотрение понятие сложного поворота. Пусть задан вектор a и тензоры поворота P1 и P2. Повернем вектор a тензором P1 и найдем вектор a′ ≡ P1 · a. Далее вектор a′ повернем тензором P2 и найдем вектор a′′ ≡ P2 · a′. В результате вектор a′′ вычисляется как сложный поворот вектора a
| a ′′ ≡ P2 · a′ = P2·P1 · a = P · a , P = P2·P1. | (45) |
Из (45) видно, что при последовательном проведении двух поворотов результирующий поворот выражается через произведение составляющих поворотов. Известно, что в общем случае произведение тензоров не коммутативно
| P2·P1 ≠ P1·P2. | (46) |
Это означает, что если произвести повороты в другом порядке, сначала P2 потом P1, то результат будет другой.
Однако не следует абсолютизировать условие (46), так как существует определенное правило квазикоммутативности (т.е. как бы перестановочности) поворотов, играющее очень важную практическую роль. В то же время это правило интуитивно понятно и расширяет поле для фантазии при описании вращения.
Пусть имеется два последовательных поворота P1 = Q(θn) и P2 = Q(φm), тогда
|
Q(φm)·Q(θn) = Q(φm)·Q(θn)·1 =
= Q(φm)·Q(θn)·QT(φm)·Q(φm). |
(47) |
Посмотрим на Q(φm)·Q(θn)·QT(φm)
|
Q(φm)·Q(θn)·QT(φm) =
= Q(φm)·[nn + cosθ(1 – nn) + sinθn × 1]·QT(φm) = = n′n′ + cosθ(1 – n′n′) + sinθn′ × 1, |
(48) |
где n′ = Q(φm) · n – повернутый вторым поворотом вектор n. В итоге получаем
| Q(φm)·Q(θn) = Q(θn′)·Q(φm). | (49) |
То есть результирующий поворот можно осуществить двумя способами. Либо сначала повернуть на угол θ вокруг n, а затем на угол φ вокруг m. Либо сначала на угол φ вокруг m, а затем на угол θ, но уже вокруг другой повернутой оси n′.
Правило
| Q(φm)·Q(θn)·QT(φm) = Q(θn′), n′ = Q(φm) · n | (50) |
полезно запомнить для проведения чисто формальных преобразований без привлечения интуиции.
Пример.
Всем известен пример из детства с юлой. В механике этот объект называется волчком Лагранжа (см. рис. 4) и представляет собой осесимметричное тело вращения с одной точкой опоры. Юла одновременно вращается вокруг собственной оси n′, которая в свою очередь вращается вокруг неподвижной вертикали m, проходящей через точку опоры.
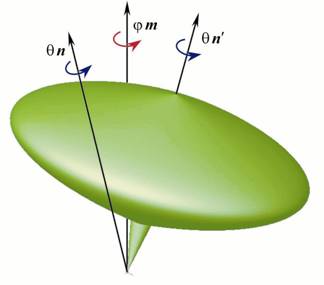
Рис. 4
На первый взгляд кажется, что наиболее удобной формой задания тензора поворота юлы является P = Q(θn′)·Q(φm). Но ведь вектор n′ непостоянный, а это в ряде случаев может существенно усложнить моделирование. Но так как n′ = Q(φm) · n, то, пользуясь правилом квазикоммутативности, мы можем написать P = Q(φm)·Q(θn), где вектор n является константой и определяет направление оси юлы в начальный момент. Второй вариант уже существенно менее затратен для моделирования. Тем не менее, при постановке задач первый способ оказывается более выигрышным.
Тензор поворота, записанный в форме P = mm + cosθ(1 – mm) + sinθm × 1, не имеет каких-либо ограничений и может применяться всегда. Тем не менее, интуитивным образом поворота является не тензор второго ранга, а некий вектор θ, называемый вектором поворота
| θ = θm, | m | = 1. | (51) |
Его направление совпадает с осью поворота m, а его модуль равен модулю угла поворота θ. В правоориентированной системе отсчета θ > 0 при взгляде с конца m, если поворот происходит против часовой стрелки. Поскольку поворот выражает реальное явление, то наличие нескольких способов его описания возможно только при условии, что способы связаны взаимно однозначным образом. Проще всего показать, что тензор поворота однозначно может быть вычислен по вектору поворота, что следует непосредственно из представления тензора поворота доставляемого теоремой Эйлера
| P = [(1– cosθ )/θ2]θθ + cosθ1 + [sinθ/θ]θ × 1. | (52) |
Видно, что последнее выражение нечувствительно к знаку θ. Поэтому величину θ в (52) можно рассматривать как модуль вектора θ, что позволяет без дополнительных соглашений однозначно вычислять тензор поворота по вектору поворота. В теории поворотов доказывается теорема, что представление (52) является ничем иным как тензорной экспонентой тензора θ × 1
| P = exp(θ × 1). | (53) |
Вам это ничем не напоминает комплексную экспоненту exp(θi), которая является оператором поворота векторов на комплексной плоскости вокруг оси перпендикулярной к ней? Общность явлений порождает общность описаний, правда со своими особенностями.
Не будем приводить здесь формулы для вычисления вектора поворота по тензору поворота, скажем лишь, что это можно также однозначно сделать. В заключение этого пункта приведем формулу для повернутого вектора a′
| a′ ≡ P(θ) · a = a + [sinθ/θ]θ × a + [(1– cosθ )/θ2]θ × (θ × a), | (54) |
использовано равенство θ × (θ × a) = θ(θ · a) – aθ2 = (θθ) · a – aθ2.
Согласно теореме Эйлера (34), любой поворот может быть осуществлен как один поворот вокруг некоторой оси на некоторый угол. Это удобно, когда ось фиксирована. Однако в большинстве задач это не так. Для эффективного решения любой задачи теории поворотов жизненно необходима следующая теорема.
Теорема. Любой поворот P(θ) может быть осуществлен в виде композиции поворотов вокруг произвольно выбираемых и фиксированных во времени осей m и n, а также оси e, выбираемой по правилу e = m × n / |m × n|,
| P(θ) = Q(ψm)·Q(Je)Q(φn). | (55) |
Изложенного выше материала вполне достаточно для того, чтобы проницательный читатель смог самостоятельно доказать данную теорему.
Если m = n, то углы ψ, J, φ называются углами Эйлера (углы прецессии, нутации и собственного вращения). Вектор e в этом случае произвольный, удовлетворяющий условию e · n = 0. Тензор поворота имеет вид
| P(θ) = Q(ψm)·Q(Je)·Q(φm). | (56) |
Однако некоторые читатели могут возразить: «Позвольте, но в учебниках по механике написано, что при использовании углов Эйлера оси как-то поворачиваются, а здесь они неподвижны…». А мы в ответ, в учебниках все правильно написано, только во всех трактовка однобокая. Вспомним правило квазикоммутативности поворотов. По нему мы можем записать
| P(θ) = Q(φm′′)·Q(Je′)·Q(ψm), | (57) |
где m′′ = Q(ψm)·Q(Je)·m = Q(Je′)·m, e′ = Q(ψm)·e. Настоятельно рекомендуем убедиться самостоятельно, что это так. Это можно сделать и формально, используя правило (50).
Видим, что в классическом представлении повороты производятся в обратном порядке и вокруг вращающихся векторов e′ и m′′. Последнее обстоятельство наиболее часто вызывает трудности в понимании и последующем восприятии углов Эйлера у многих студентов.
На практике помимо углов Эйлера используется масса других систем углов. Наиболее известны «самолетные» и «корабельные» углы. О них мы расскажем в следующих статьях. А сейчас рассмотрим небольшой пример.
Пример.
Многие, наверное, смотрели фильм «Косильщик лужаек». Там есть одна сцена, где главного героя раскручивают в непонятной машине, представляющей собой три скрепленных кольца, во внутреннее кольцо был помещен наш герой. В механике подобный механизм называется трехстепенным гироскопом и схематично изображен на рис. 5. Три кольца – внутреннее зеленое, среднее красное, наружное синее – соединены так, что внутреннее кольцо может свободно вращаться относительно среднего вокруг оси m′′, среднее кольцо вращается относительно внешнего вокруг оси e′, внешнее же кольцо вращается вокруг неподвижной оси n.
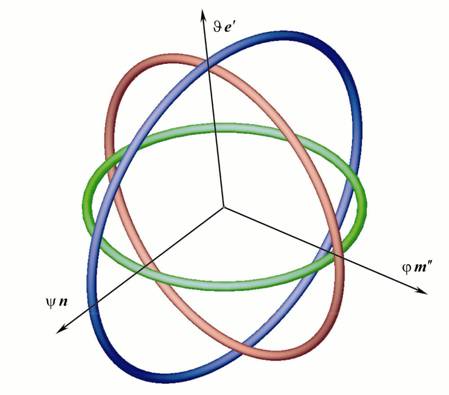
Рис. 5
Ответим на вопрос, как можно задать ориентацию объекта, жестко закрепленного во внутреннем кольце. Раз жестко, то достаточно написать тензор поворота для внутреннего кольца. Всего существует шесть возможных эквивалентных вариантов задания результирующего поворота. Мы же выберем наиболее очевидный вариант
|
P = Q(φm′′)·Q(Je′)·Q(ψn),
e′ = Q(ψn) · e, m′′ = Q(Je′)·Q(ψn) · m = Q(ψn)·Q(Je) · m, |
(58) |
где e, m – орты направления осей вращения в отсчетном положении (в начальный момент времени).
Обратите внимание, что мы не стали долго думать, как же подстроить эйлерову систему углов для нашей задачи, а, просто глядя на задачу, сходу написали ответ. Именно последнее обстоятельство является тем огромным преимуществом прямого тензорного языка при описании поворотов, которое заставляет приложить минимум усилий для его изучения с целью максимальной практической отдачи. Рекомендуем читателю получить остальные 5 вариантов представления тензора P.
Вот мы и добрались до самого интересного места этой статьи. А именно, до связи тензора поворота с еще одним замечательным объектом – кватернионом поворота. Для начала перепишем формулу (54) для повернутого вектора a′ используя функции половинного аргумента и вернувшись обратно к записи через вектор m
|
a′ =
a + sinθm × a
+ (1 – cosθ)m ×
(m × a) =
= a + 2sin(θ/2)cos(θ/2)m × a + 2sin2(θ/2) m × (m × a). |
(59) |
Введем обозначения
| λ0 = cos(θ/2), λ = sin(θ/2)m. | (60) |
Полезное свойство данных обозначений
| (λ0)2 + |λ|2 = (λ0)2 + λ · λ = 1. | (61) |
Выражение (59) можно переписать в виде
|
a′ =
a + 2λ0λ
× a + 2λ
× (λ × a) =
= (λ0)2a + λ(λ · a) + 2λ0λ × a + λ × (λ × a). |
(62) |
Найдем далее выражение вектора поворота композиции двух поворотов
| Q(θ) = Q(φ)·Q(ψ). | (63) |
Для этого воспользуемся формулой (52), записанной также через функции половинного аргумента и введенные обозначения (60)
|
P =
2sin2(θ/2)mm
+ 2[cos2(θ/2)
– 1/2]1
+ 2sin(θ/2)cos(θ/2)m
× 1 =
= 2{λλ + [(λ0)2 – 1/2]1 + λ0λ × 1} |
(64) |
Сопоставим векторам φ и ψ пары
| μ0 = cos(|φ|/2), μ = sin(|φ|/2)φ /|φ |, | (65) |
| ν0 = cos(|ψ|/2), ν = sin(|ψ|/2)ψ /|ψ|. | (66) |
Подставив данные выражения в (63), получим
|
Q(θ) =
Q(φ)·Q(ψ) =
= 4{μμ + [(μ0)2 – 1/2]1 + μ0μ × 1}·{νν + [(ν0)2 – 1/2]1 + ν0ν × 1}= = 4{μν(μ · ν) + μμ[(ν0)2 – 1/2] + ν0μμ × ν + + νν[(μ0)2 – 1/2] + [(μ0)2 – 1/2] [(ν0)2 – 1/2]1 + [(μ0)2 – 1/2] ν0ν × 1 + + μ0μ × νν + [(ν0)2 – 1/2]μ0μ × 1 + μ0ν0μ × 1 × ν} = = 2{λλ + [(λ0)2 – 1/2]1 + λ0λ × 1} |
(67) |
Напомним, что для любых векторов b и c справедливы равенства
| b × 1 = 1 × b = – (b × 1)T, tr(b × 1) = 0, tr(b × cc) = (b × c) · c = 0, |
| tr(cc) = c · c, b × 1 × c = cb – (c · b)1, tr(b × 1 × c) = – 2(c · b), |
| (b × 1)× = –2b, (b × cc)× = (b × c) × c = c(b · c) – b(c · c), (cc)× = 0, (b × 1 × c)× = c × b. |
Взяв след и векторный инвариант от обеих частей равенства (67) и проведя нехитрые алгебраические преобразования, получим достаточно простые выражения, позволяющие вычислить вектор поворота композиции двух поворотов
| λ0 = μ0ν0 – μ · ν, | (68) |
| λ = μ0ν + ν0μ + μ · ν. | (69) |
Далее можно ввести множество объектов, представляющих собой пару Λ = (λ0, λ), на котором задан закон композиции элементов (операция умножения), в соответствии с формулами (68, 69).
Можно убедиться, что данный закон умножения является ассоциативным (Λ·Μ)·Ν = Λ·(Μ·Ν), дистрибутивным (Λ + Μ)·(Ν + Ρ) = Λ·Ν + Λ·Ρ + Μ·Ν + Μ·Ρ и удовлетворяет условию (αΛ)·(βΜ) = αβΛ·Μ, где α, β– произвольные вещественные числа. Операция суммы вводится следующим образом Λ + Μ = (λ0, λ) + (μ0, μ) = (λ0 + μ0, λ + μ). В математике данное множество называется алгеброй кватернионов, а сами объекты кватернионами. Выше нами были рассмотрены кватернионы единичной длины (λ0)2 + λ · λ = 1, которые наравне с тензором поворота могут использоваться для задания ориентации тела в трехмерном пространстве. В общем случае кватернионы могут иметь произвольную длину. Более подробно о кватернионах и о том, как их использовать для описания поворотов, будет написано Zed’ом в следующем номере журнала.
Выше был рассмотрен достаточно простой с формальной точки зрения и в то же время интуитивно понятный математический объект как тензор конечного поворота. Мы надеемся, что наша статья приоткрыла для читателя завесу таинственности и непонятности в вопросе описания произвольных поворотов в трехмерном пространстве. Как было сказано во введении, мы намеренно уклонились от вычислительных аспектов данной проблемы, желая разбудить у читателя интуицию. В следующей статье мы расскажем о координатной форме представления тензора поворота – матрице поворота. Что позволит читателю реализовать в программном коде примеры из данной статьи и множество собственных еще не родившихся идей. При этом он будет делать это, мы надеемся, с глубоким пониманием происходящего.
Тем не менее, читатель уже сейчас имеет такое мощное вычислительное средство как кватернион поворота. Этот объект интуитивно также прост для восприятия, как и тензор поворота. На сегодняшний день он является реальным конкурентом классическим матрицам поворота. Поэтому для всестороннего понимания поворотов читатель должен в итоге уметь свободно обращаться с двумя объектами: тензором поворота и кватернионом поворота.